Review
In the previous section, we know that the CRF layer can learn some constraints from the training dataset to ensure the final predicted entity label sequences are valid.
The constrains could be:
- The label of the first word in a sentence should start with “B-“ or “O”, not “I-“
- “B-label1 I-label2 I-label3 I-…”, in this pattern, label1, label2, label3 … should be the same named entity label. For example, “B-Person I-Person” is valid, but “B-Person I-Organization” is invalid.
- “O I-label” is invalid. The first label of one named entity should start with “B-“ not “I-“, in other words, the valid pattern should be “O B-label”
- …
After you read this article, you will know why the CRF layer can learn those constrains.
2. CRF Layer
In the loss function of CRF layer, we have two types of scores. These two scores are the key concepts of CRF layer.
2.1 Emission score
The first one is the emission score. These emission scores come from the BiLSTM layer. As shown in figure 2.1, for example, the score of $ w_0 $ labeled as B-Person is 1.5.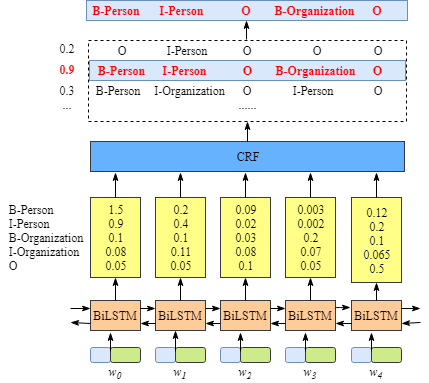
For convenience, we will give each label a index number as shown in the table below.
| Label | Index |
|---|---|
| B-Person | 0 |
| I-Person | 1 |
| B-Organization | 2 |
| I-Organization | 3 |
| O | 4 |
We use $ x_{iy_j} $ to represent the emission score. $ i $ is the index of word and $ y_j $ is the index of label. For instance, according the figure 2.1, $ x_{i=1,y_j=2} = x_{w_1,B-Organization} = 0.1$ which means the score of $ w_1 $ as B-Organization is 0.1.
2.2 Transition score
We use $ t_{y_iy_j} $ to represent a transition score. For example, $ t_{B-Person, I-Person} = 0.9$ means the score of label transition $ B-Person \rightarrow I-Person$ is 0.9. Therefore, we have a transition score matrix which stores all the scores between all the labels.
In order to make the transition score matrix more robust, we will add two more labels, START and END. START means the start of a sentence, NOT the first word. END means the end of sentence.
Here is an example of the transition matrix score including the extra added START and END labels.
| START | B-Person | I-Person | B-Organization | I-Organization | O | END | |
|---|---|---|---|---|---|---|---|
| START | 0 | 0.8 | 0.007 | 0.7 | 0.0008 | 0.9 | 0.08 |
| B-Person | 0 | 0.6 | 0.9 | 0.2 | 0.0006 | 0.6 | 0.009 |
| I-Person | -1 | 0.5 | 0.53 | 0.55 | 0.0003 | 0.85 | 0.008 |
| B-Organization | 0.9 | 0.5 | 0.0003 | 0.25 | 0.8 | 0.77 | 0.006 |
| I-Organization | -0.9 | 0.45 | 0.007 | 0.7 | 0.65 | 0.76 | 0.2 |
| O | 0 | 0.65 | 0.0007 | 0.7 | 0.0008 | 0.9 | 0.08 |
| END | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
As shown in the table above, we can find that the transition matrix has learned some useful constrains.
- The label of the first word in a sentence should start with “B-“ or “O”, not “I-“ (The transtion scores from “START” to “I-Person or I-Organization” are very low.)
- “B-label1 I-label2 I-label3 I-…”, in this pattern, label1, label2, label3 … should be the same named entity label. For example, “B-Person I-Person” is valid, but “B-Person I-Organization” is invalid. (For example, the score from “B-Organization” to “I-Person” is only 0.0003 which is much lower than the others.)
- “O I-label” is invalid. The first label of one named entity should start with “B-“ not “I-“, in other words, the valid pattern should be “O B-label” (Again, for instance, the score $t_{O,I-Person}$ is very small.)
- …
You may want to ask a question about the matrix. Where or how to get the transition matrix?
Actually, the matrix is a paramer of a BiLSTM-CRF model. Before you train the model, you could initialize all the transition scores in the matrix randomly. All the random scores will be updated automatically during your training process. In other words, the CRF layer can learn those constraints by itself. We do not need to build the matrix manually. The scores will be more and more reasonable gradually with increasing training iterations.
Next
2.3 CRF loss function
Introduction of CRF loss function which is consist of the real path score and the total score of all the possible paths.
2.4 Real path score
How to calculate the score of the true labels of a sentence.
2.5 The score of all the possible paths
How to calculate the total score of all the possible paths of a sentence with a step-by-step toy example.
References
[1] Lample, G., Ballesteros, M., Subramanian, S., Kawakami, K. and Dyer, C., 2016. Neural architectures for named entity recognition. arXiv preprint arXiv:1603.01360.
https://arxiv.org/abs/1603.01360
Note
Please note that: The Wechat Public Account is available now! If you found this article is useful and would like to found more information about this series, please subscribe to the public account by your Wechat! (2020-04-03)
When you reprint or distribute this article, please include the original link address.